PERSAMAAN GARIS

A. Pengertian Persamaan Garis Lurus
1. Koordinat cartesius
Gambarlah koordinat cartesius yang memiliki sumbu mendatar (disebut sumbu x) dan sumbu mendater (disebut sumbu y). Titik potong kedua sumbu tersebut dinamakan titik asa atau titik pusat koordinat. Pada gambar ini titik pusat koordinat cartesius ditunjukkan oleh titik O ( 0,0 ).


a. Menggambar titik pada kordinat cartesius
Setiap titik pada bidang cartesius dinyatakan dalam pasangan berurutan x dan y, dimana x merupakan koordinat sumbu x ( disebut absis ) dan y merupakan koordinat. Jadi titik pada bidang koordinat cartesius dapat dituliskan ( x,y ). Contoh gambar titik pada koordinat cartesius dengan menggunakan aturan penulisan titik koordinat. Misalkan titik A ada 6 titik koordinat.

 Titik A (x,y) → A (2,1)
 Titik B (x,y) → B (-2,3)
 Titik C (x,y) → C (-3,-1)
 Titik D (x,y) → D (4,-3)
 Titik E (x,y) → E (3,0)
 Titik F (x,y) → F (0,2)



b. Menggambar garis pada koordinat cartsius
Setelah memahami bagaimana cara menggambar titik pada bidang koordinat cartesius. Sekarang bagaimana cara menggambar garis lurus pada bidang yang sama.
(a) (b)



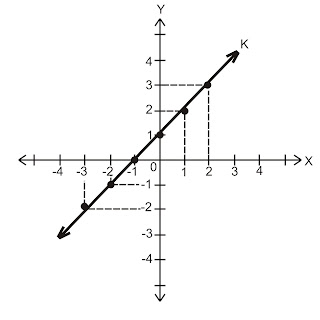
Yang perlu diingat, garis lurus adalah kumpulan titik-titik yang letaknya sejajar. Dari gambar A terlihat bahwa titik P.Q.R.S.T. dan U memiliki letak yang sejajar dengan suatu garis lurus, misalkan garis K seperti digambarkan pada gambar b.
Sebuah garis lurus dapat terbentuk dengan syarat sedikitnya ada 2 titik pada bidang koordinat cartesius.

2. Menggambarkan Persamaan Garis Lurus
Setelah mempelajari materi sebelumnya maka kita dapat menyimpulkan bahwa persamaan garis lurus adalah suatu persamaan yang jika digambarkan ke dalam bidang koordinat cartesius akan membentuk sebuah garis lurus. Cara menggambar persamaan garis lurus adalah dengan menentukan nilai x dan y secara acak. Perlu diingat bahwa 2 titik sudah cukup untuk membuat garis lurus pada bidang koordinat cartesius.
Contoh soal :
Gambarlah garis dengan persamaan :
a. x + y = 4
b. x = 2y
Jawab :
a. langkah pertama adalah menentukan nilai x dan y yang memenuhi persamaan x + y = 4
misalkan : x = 0 maka 0 + y = 4 → y = 4, sehingga diperoleh titik koordinat ( 0,4 ) x = 3 maka 3 + y = 4 → 1 sehingga diperoleh titik koordinat ( 3,1 )
kemudian dari dua titik koordinat tersebut dapat digambarkan garis lurus seperti berikut :


b. Sebelumnya tentukan dulu nailai x atau y yang memenuhi persamaan x = 2y
Misalkan : x = 0 maka 0 = 2y → y = 0 Sehingga diperoleh titik koordinat (0,0)
x = 4 maka 4 = 2y → y = 2. sehingga diperoleh titik koordinat (4,2)
Kedua titik tersebut dapat digambar menjadi sebuah garis lurus sebagai berikut :






Bentuk umum persamaan garis lurus :




B. Gradien
1. Pengertian Gradien
Gradien adalah tingkat kemiringan garis atau slofe atau gradien juga merupakan perbandingan antara vertikal dan horizontal.
2. Perhitungan Gradien
Ada beberapa cara untuk menghitung gradien dan satu persamaan garis lurus. Hal ini tergantung pada letak titik koordinat dan bentuk persamaan garis yang diberikan.
a. Menghitung gradien pada persamaan garis y = mx seperti yang telah di jelaskan bahwa gradien suatu garis dapat ditentukan melalui perbandingan antara ordinat dan absis. Dapat ditulis sebagai berikut :
Gradien =
m =
y = mx
Dari uraian ini terlihat bahwa nilai gradien dalam satu persamaan garis sama dengan besar nilai konstantan m yang terletak di depan variabel x dengan syarat persamaan garis tersebut di ubah terlebih dahulu ke dalam bentuk y = mx.
Contoh soal !
Tentukanlah gradien dari persamaan garis berikut :
a. y = 2x
b. 2x + 3y = 0
Jawab :
a. Persamaan garis y = 2x sudah memenuhi bentuk y = mx, maka y = 2x, jadi diperoleh m = 2
b. Persamaan garis 2x + 3y = 0, di ubah terlebih dahulu menjadi bentuk y = mx. sehingga :
2x + 3y = 0
3y = -2x
y = , jadi diperoleh m =

b. Menghitung gradien pada persamaan garis y = mx + c
Sama halnya dengan perhiungan gradien pada persamaan garis y = mx, perhitungan gradien pada garis y = mx + c dilakukan dengan cara menentukan nilai konstanta di depan variabel x.
Contoh soal :
Tentukan gradien dari persamaan garis berikut
a. y = -5x - 8
b. 2 + 4y = 3x + 5
c. 3y = 6 + 9x
jawab :
a. Persamaan garis y = -5x – 8 sudah memenuhi bentuk y = mx + c jadi nilai m = -5
b. Persamaan garis 2 + 4y = 3x + 5 diubah terlebih dahul menjadi bentuk y = mx + c sehingga :
2 + 4y = 3x + 5
4y = 3x + 5 – 2
4y = 3x + 3
y =
y = , jadi nilai m =
c. Persamaan garis 3y = 6 + 9x diubah terlebih dahulu menjadi bentuk y = mx + c, sehingga :
3y = 6 + 9x
y =
y = 2 + 3x
y = 3x + 2 , jadi nilai m = 3

c. Menghitung gradien pada Persamaan Garis ax + by + c = 0
Sama seperti sebelumnya, gradien pada persamaan garis ax + by + c = 0 dapat ditentukan dengan cara mengubah terlebih dahulu persamaan garis tersebut kedalam bentuk y = mx + c kemudian nilai gradien dapat diperoleh dari nilai konstanta m di depan variabel x.
Contoh soal !
Tentukan gradien dari persamaan garis berikut :
a. x + 2y + 6 = 0
b. 2y – 6x + 1 = 0
c. 4x + 5y = 9
Jawab :
a. Persamaan garis x + 2y + 6 = 0 diubah terlebih dahulu menjadi bentuk y = mx + c. sehingga :
x + 2y + 6 = 0
2y = -x – 6
y =
y = - x – 3 , jadi nilaim = -
b. Persamaan garis 2y – 6x + 1 = 0 diubah terlebih dahulu menjadi bentuk y = mx + c. sehingga :
2y – 6x + 1 = 0
2y = 6x – 1
y =
y =
y = 3x - , jadi nilai m = 3
c. Persamaan garis 4x + 5y = 9 diubah terlebih dahulu menjadi bentuk y = mx + c. sehingga :
4x + 5y = 9
5y = 9 – 4x
y =
y =
y = , jadi nilai m =

d. Menghitung gradien pada garis yang memenuhi dua titik


Gambar diatas tersebut menunjukan sebuah garis lurus pada bidang koordinat yang melalui titik P dan R. Untuk mencari gradien tersebut kita tinggal menentukan gradien PR pada segitiga PQR dengan menggunakan perbandingan ordinat dan absis, maka akan diperoleh gradien garis yang melalui titik P dan R yaitu :
Garadien PR =
m PR =
m PR =
=
=
Jadi gradien garis yang melalui P (1,3) dari R (7,6) pada gambar di atas adalah
Dari uraian diatas dapat diperoleh rumus umum untuk mencari gradien pada garis yang melalui dua titik sebagai berikut :




Contoh soal !
Tentukanlah gradien garis yang melalui titik-titik koordinat berikut :
a. A (2,2) dan B (4,4)
b. C (3,1) dan D (2,4)
Jawab :
a. Untuk titik A (2,2) maka x1 = 2, y1 = 1
Untuk titik B (4,4) maka x2 = 4, y2 = 4
m =
=
= = 1
jadi gradiennya adalah 1.

b. Untuk titik C (3,1) maka x1 = 3, y1 = 1
untuk titik D (2,4) maka x2 = 2, y2 = 4
m =
=
= = -3
jadi gradiennya adalah -3


3. Sifat-sifat gradien
a. Gradien garis yang sejajar sumbu x

Pada gambar diatas terlihat garis k yang melalui titik A (-1,2) dan B (3,2). Garis tersebut sejajar dengan sumbu x. Untuk menghitung gradien garis k gunakan cara sebagai berikut :
Untuk titik A (-1,2) maka x1 = -1, y1 = 2
Untuk titik B (3,2) maka x2 =3, y2 = 2
m =
=
= = 0
Dapat diambil kesimpulan bahwa :


b. Gradien garis yang sejajar sumbu y
Pada gambar diatas l yang melalui titik C (1,3) dan D (1,-1) letaknya sejajar dengan sumbu y, gradien garis tersebut adalah sebagai berikut :
Untuk titik C (1,3) maka x1 = 1, y1 = 3
Untuk titik D (1,-1) maka x2 = 1, y2 = -1
m =
=
= , tidak terdefinisi
maka dalam perhitungan diatas dapat diambil kesimpulan bahwa :


c. Gradien dua garis sejajar

Garis k dan l merupakan dua garis yang sejajar, maka untuk mencari kedua garis gradien tersebut perhatikan uraian berikut :
 Untuk garis k melalui A (-2,0) dan B (0,2)
untuk A (2,0) maka x1 = -2 , y1= 0
untuk B (0,2) maka x2 = 0 , y2 = 2
mAB =
=
=
= 1
 Untuk garis l melalui titik C (0,-1) dan D (1,0)
untuk titik C (0,-1) maka x1 = 0 , y1 = -1
untuk titik D (1,0) maka x2 = 1 , y2 = 0
mCD =
=
=
= 1
Dari uraian diatas kita dapat mengambil kesimpulan bahwa :


d. Gradien dua garis yang tegak lurus








Gradien kedua garis tersebut dapat dihitung dengan cara sebagai berikut :
 Garis k melalui titik C (3,0) dan D (0,3)
untuk titik C (3,0) maka x1 = 3, y1 = 0
untuk titik D (0,3) maka x2 = 0, y2 = 3
mCD =
=
= = -1
 Garis l melalui titik A (-1,0) dan B (0,1)
untuk titik A (-1,0) maka x1 = -1, y1 = 0
untuk titik B (0,1) maka x2 = 0, y2 = 1
mAB =
=
=
= 1
Hasil kedua gradien tersebut kemudian dikalikan sebagai berikut
mAB . mCD = 1 . -1
= -1
Dari uraian diatas dapat diambil kesimpulan bahwa :


Atau dapat ditulis

C. Menentukan Persamaan Garis Lurus
Bentuk y = mx merupakan persamaan garis lurus yang paling sederhana karena garis yang dibentuk oleh persamaan garis tersebut selalu melalui titik pusat koordinat. Adapun bentuk umum dari persamaan garis lurus dapat ditulis sebagai berikut.


Persamaan garis ini hampir sama dengan bentuk sederhananya. Namun diberi tambahan konstanta (lambang c). Hal ini menunjukan bahwa garis yang dibentuk oleh persamaan garis tersebut tidak akan melalui titik 0 (0,0).
Ada beberapa cara dalam menentukan sebuah persamaan garis dari gradien dari titik koordinat / gradien.

1. Menentukan persamaan garis dari gradien dan titik koordinat










Dari gambar diatas, garis tersebut melalui titik A (x1,y1) dan tidak melalui titik pusat koordinat sehingga persamaan garis pada gambar tersebut dapat dituliskan :
y1 = mx1 + c . . . (1)
Adapun bentuk umum persamaan garis yang tidak melalui titik pusat koordinat dituliskan :
y = mx + c . . . (2)
Dari persamaan (2) dan persamaan (1) dapat ditentukan selisih yaitu :
y = mx + c
y1 = mx1 = c _
y - y1 = mx – mx1 + c – c
y – y1 = m (x – x1)
maka dapat diperoleh rumus umum untuk menentukan persamaan garis, yaitu :

Contoh soal :
Tentukan persamaan garis yang melalui titik P ( 3,5 ) dan memiliki gradien -2
Jawab :
Untuk titik P ( 3,5 ) maka x1 = 3, y1 = 5
Dengan menggunakan rumus umum, diperoleh persamaan garis :
y - y1 = m (x – x1)
y – 5 = -2 (x – 3 )
y – 5 = -2x + 6
y = -2x + 6 + 5
y = -2x + 11 atau
2x + y -11 = 0
2. Menentukan persamaan garis yang melalui dua titik
Untuk menentukan persamaan garis yang melalui dua titik, karena caranya hampir sama dengan rumus umum yang telah dipelajari sebelumnya.
Perhatikan uraian berikut
 y – y1 = m (x – x1) adalah rumus persamaan garis dari gradien dan titik koordinat

 m = adalah rumus gradien dari dua titik koordinat
dari kedua rumus tersebut dapat diuraikan sebagai berikut.
y –y1 = m (x – x1)
y – y1 = (x – x1)
y –y1 =


Jadi, rumus untuk menentukan persamaan garis yang melalui dua titik koordinat adalah :


Contoh soal !
Tentukan persamaan garis yang melalui titik koordinat A (3,3) dan B (2,1)
Jawab :
Untuk titik A (3,3) maka x1 = 3, y1 = 3
Untuk titik B (2,1) maka x2 = 2, y2 = 1
Persamaan yang diperoleh



-1 (y – 3) = -2 (x – 3)
-y + 3 = -2x + 6
2x – y + 3 – 6 = 0
2x – y -3 = 0
Jadi persamaan garisnya adalah 2x – y – 3 = 0
3. Menentukan koordinat titik potong dari dua garis lurus


(a) garis k dan l yang sejajar
(b) garis k dan l yang berpotongan di A.


Cara menentukan koordinat titik potong dari persamaan garis yaitu dengan cara :
a. Grafik
Dengan cara ini dua persamaan garis digambar kedalam bidang koordinat cartesius sehingga koordinat titik potong kedua garis tersebut dapat dilihat dari gambar.
Contoh soal !
Tentukan titik potong antara garis 3x + y = 5 dan garis 2x – 3y = 7 dengan cara grafik?
Jawab :
 Garis 3x + y = 5
Untuk x = 1, maka y = 2, sehingga diperoleh ttitik (1,2)
Untuk x = 0, maka y = 5, sehingga diperoleh titik (0,5)
 Garis 2x – 3 = 7
Untuk x = 5, maka y = 1, sehingga diperoleh titik (5,1)
Untuk x = -1, maka y = -3, sehingga diperoleh titik (-1,-3)
Kemudian gambarlah grafik dari titik-titik yang didapat tersebut.


dari gambar dapat dilihat bahwa koordinat titik potong garis tersebut adalah titik A (2,-1).
b. Substitusi
Dengan cara substitusi, salah satu variabel dari persamaan garis yang diketahui dimasukan (disubstitusikan) kedalam variabel yang sama dan persamaan garis yang lain.
Contoh soal !
Tentukan koordinat titik potong 3x + y = 5 dan garis 2x - 3y = 7 dengan cara substitusi.
Jawab :
Ikuti langkah berikut :
 Ambil salah satu persamaan garis misalnya 3x + y = 5
 Tentukan salah satu variabel dari garis tersebut misalnya y → 3x + y = 5 maka y = 5 – 3x
 Substitusikan nilai y tersebut kedalam persamaan garis yang lain.
 2x – 3y = 7
2x – 3 (5 – 3x) = 7
2x – 15 + 9x = 7
2x + 9x = 7 + 15
11x = 22
x =
x = 2
 Subtitusikan nilai x kedalam salah satu persamaan garis
3x + y = 5
3(2) + y = 5
6 + y = 5
y = 5-6
y = -1
Diperoleh x = 2 dan y = -1
Jadi koordinat titik potong kedua garis itu adalah (2,-1)